Optimal Grasps and Placements for Task and Motion Planning in Clutter
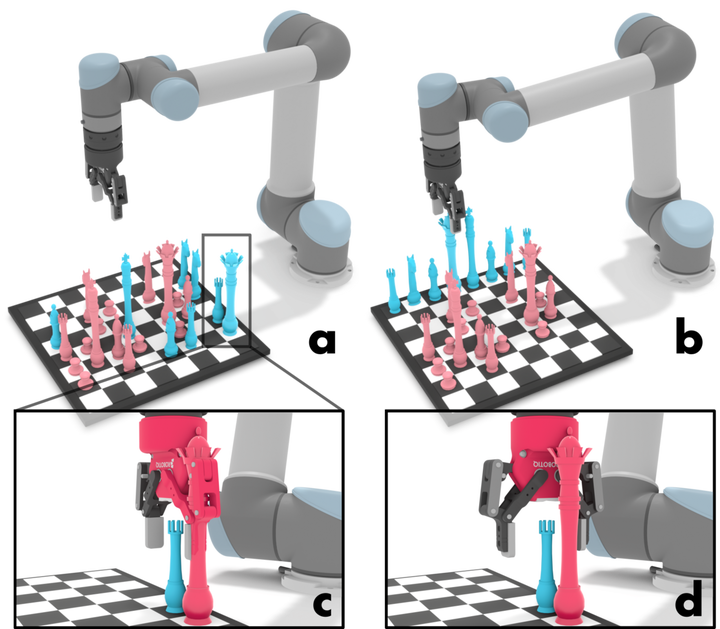 A cluttered manipulation scenario. a) Example start configuration. b) Example of goal configuration. c-d) Example of action infeasibility from clutter
A cluttered manipulation scenario. a) Example start configuration. b) Example of goal configuration. c-d) Example of action infeasibility from clutter
Planning for sequential manipulation in robotics is paramount. This is typically achieved by a layered planning approach (called Task and Motion Planning - TAMP) where a skeleton is computed by a task planner first and then the robot motions for the actions within this skeleton are computed by a motion planner. Before the motions can be computed, continuous values of the action parameters need to be first resolved (this is called grounding). For example, to compute the motion to pick up an object, the grasp pose (i.e. the relative pose of the robot’s end-effector with respect to the object) needs to be computed first. To place an object in a surface, the new object location is required. Most TAMP frameworks rely on specialized samplers to obtain these parameters and they do not consider complex geometric constraints that can arise in the presence of cluttered environments. We contribute a specialized grounder for placements and grasps that considers all the actions of a plan skeleton jointly for problems of planar manipulation under heavy cluttered scenes.
Our grounder is designed to solve problems of planar manipulation, where the robot is required to pick up and place a sequence of objects on a surface and there is potentially many objects of different heights. Additionally, we argue that these problems are hard because they have a very little amount of free space to be used as intermediate placement locations for objects. This setup is similar to a problem known as Object Rearrangement (OR), but unlike OR, we do not assume action feasibility, i.e., the robot hand may collide with another object when placing the grasped object due to their geometry. Additionally, our setup considers other scenarios where objects can be stacked on top of other objects (i.e., high-level actions other than pick and place are considered).
Our solution
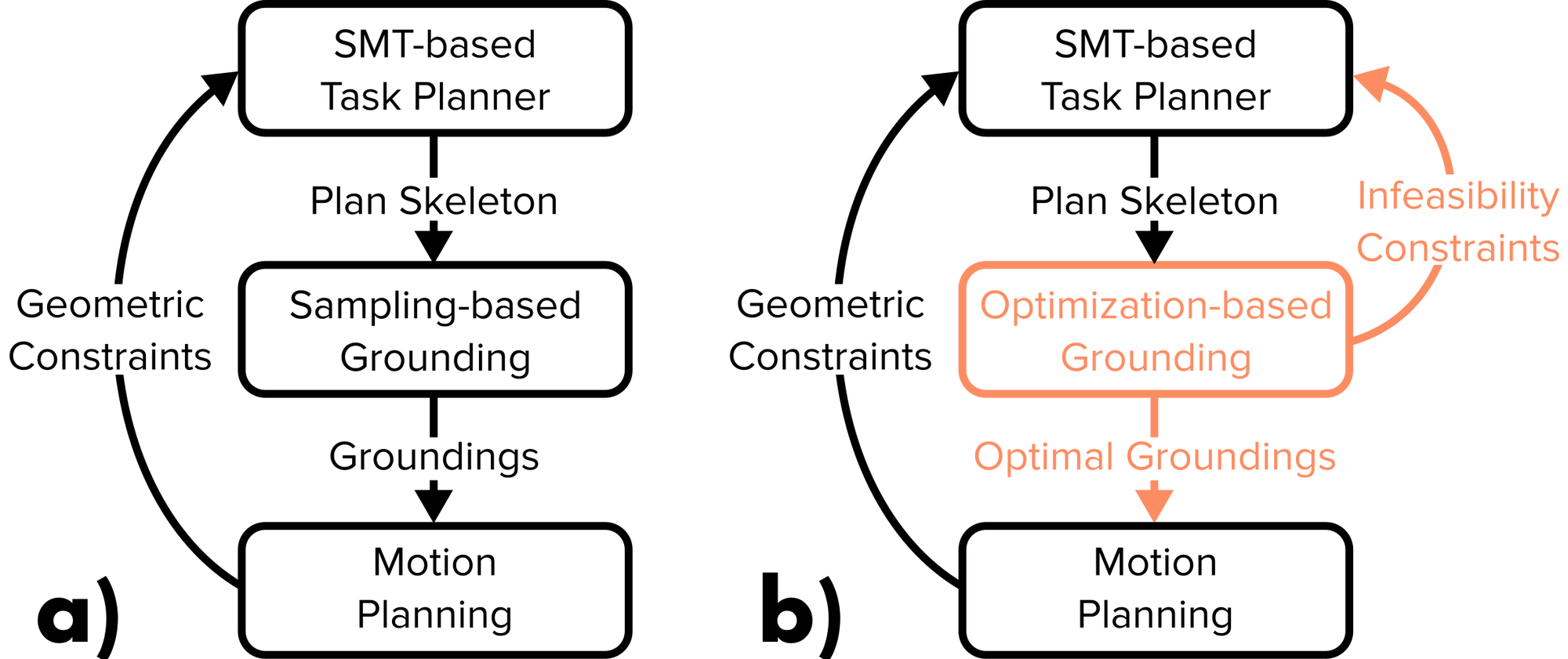
To solve these problems we propose a specialized grounder that is formulated as an optimization problem over the joint variables of candidate plan skeletons. We describe feasibility constraints (no collision) as non overlapping primitive shapes over conservative approximations of the projections of the robot hand and the objects (see figure below). By performing this simplification, we are able to write problems that can be solved up to global optimality very efficiently. Furthermore, infeasibility of our optimization formulations provides useful information that we use to prune the task space to find plan skeletons that are more likely to be feasible.
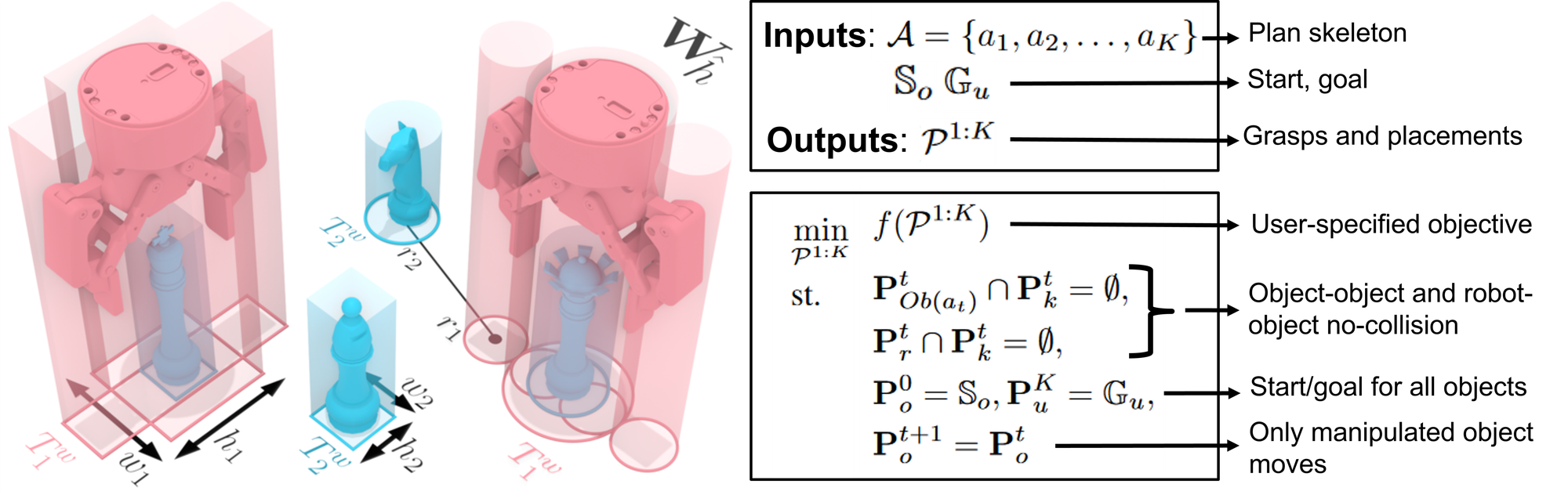
Challenging problems
The proposed problems are hard due to the high clutter and small amount of free space to place objects. Additional geometric constraints arise when the robot tries to pick up a short object next to a tall object since the robot geometry may collide with the neighbor object.
- Obstructed Pick X (OP-X): a short object that is surrounded by tall objects needs to be grasped and placed in a given goal location. All other objects doe not have a specified goal. This experiment is increasingly hard for high values of X and we show up to OP-9.
- Chessboard (Chess): The robot needs to set up the blue pieces of the chess in the starting configuration. For each piece, we compute a cylinder that fully contains the mesh representation to express the feasibility constraints and use the circle of its base as geometric primitive.
- Tower Assembling (Tower): The robot needs to assemble a tower with three blocks at a goal location in the given order. Before that, the objects are stacked and therefore they need to be unstacked first. When unstacking them, intermediate locations are needed and other objects on the surface need to be avoided. This is an example of a task that involves highl-level actions other than pick and place (stack and unstack).