Robust Motion Planning under Sensing Uncertainty
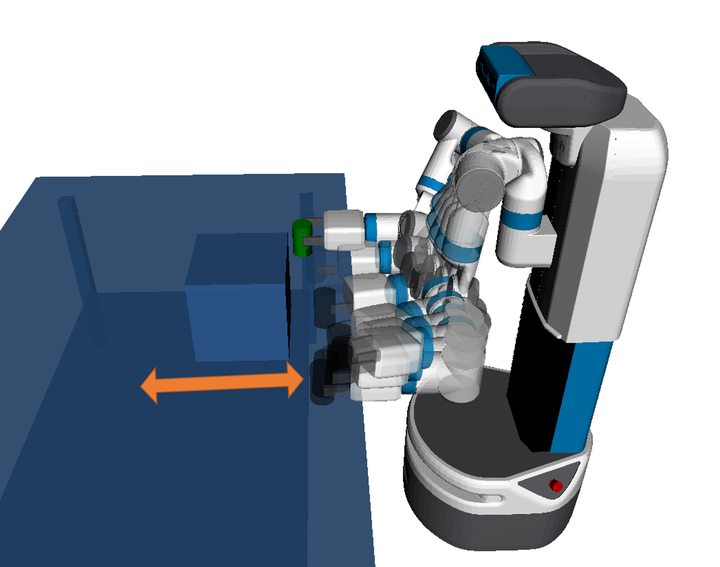 Planning a robust trajectory for the Fetch robot when obstacles are uncertain in their poses
Planning a robust trajectory for the Fetch robot when obstacles are uncertain in their poses
Motion planning for high degree-of-freedom ( DOF ) robots is challenging, especially when acting in complex environments under sensing uncertainty. While there is significant work on how to plan under state uncertainty for low- DOF robots, existing methods cannot be easily translated into the high-DOF case, due to the complex geometry of the robot’s body and its environment.
The figure above shows an example of a Fetch robot performing manipulation tasks in a table environment. The objects on top of the table are subject to sensing uncertainty in the direction shown by the arrow. The objective is to find a plan to move the green can from its starting position (to the left of the robot) to its goal position, while taking into account the object’s uncertainty. The shown trajectory was computed by our proposed method Robust Optimization-based Motion Planner (ROMP).
When we have perfect information about the location of objects in a given scene, motion planning methods provide an efficient way to solve our high-DOF manipulation problem. Sampling-based and Optimization-based methods stand out for this task. The former methods, build connectivity information in the robot’s configuration space by means of random sample and use such information to find a path between start and goal. The latter methods optimize cost functions that encourage smooth trajectories constrained to stay collision-free. RRT-Connect and TrajOpt are representatives of each category.
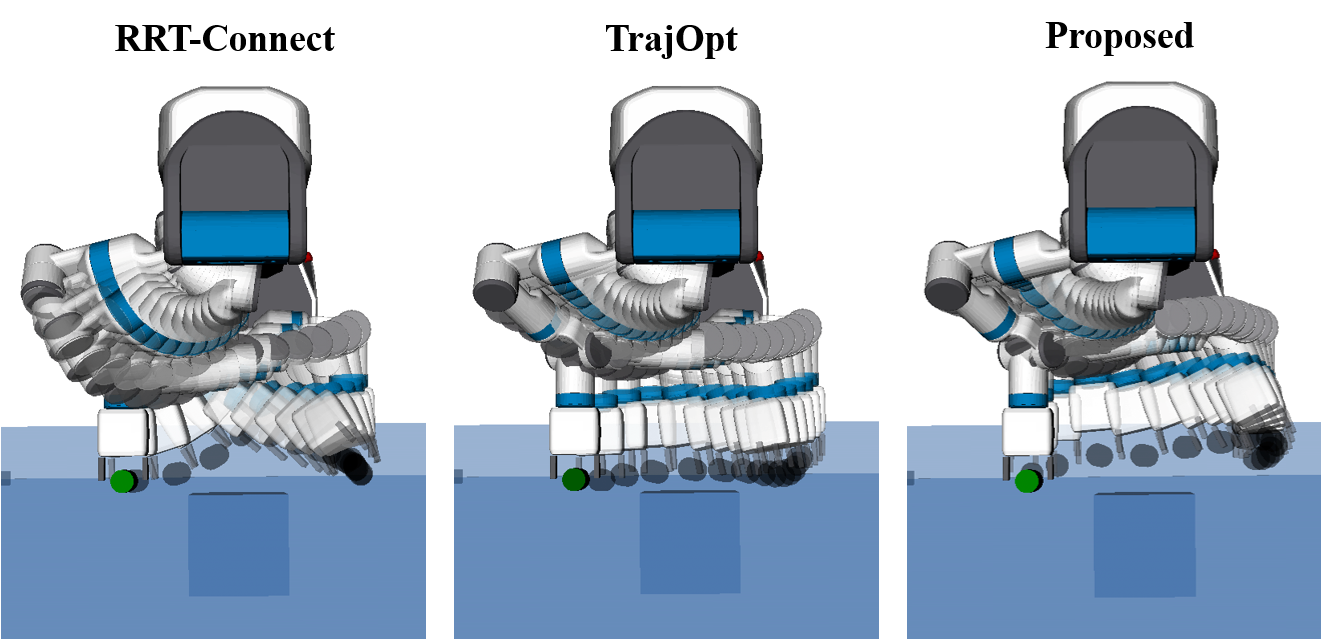
The figure below shows top views of Fetch trajectories found by RRT-Connect, TrajOpt and the proposed ROMP, for our manipulation example. Importantly for this application, all planners generate trajectories that go close to the noisy obstacle. This is achieved by using a shortcut heuristic to the plan returned by RRT-Connect. TrajOpt on the other hand naturally encourages short trajectories. It can be seen that ROMP’s trajectory stays further away from the noisy object.
The target here is not to compare the proposed approach with existing methods. That would not be a fair comparison since they are unaware of the obstacles’ uncertainty. Our objective is to provide a method to incorporate this type of uncertainty when planning and highlight its benefits compared to not taking the uncertainty into account.
How does ROMP work?
ROMP can be thought of as an extension of optimization-based planners to account for uncertainty information. It is based on sequential convex optimization (SCO), where the non-convex collision avoidance constraints are linearized around the current solution and a quadratic program is solved at every iteration. A key difference with respect to optimization-based uncertainty unaware planners (e.g., TrajOpt) is that at every iteration of the SCO problem, ROMP creates a robust optimization formulation that protects the solution of the convex subproblem to uncertainty in the problem parameters. The uncertainty of this parameters comes from the uncertainty in the signed distance function between the noisy obstacle and the robot’s links and is assumed to be bounded. In its current version, the uncertain parameters lie in a cardinality constrained set.
Two important aspects make ROMP attractive to be used for robust motion planning. On one hand, it can be applied to high-DOF robots since its formulation leverages the signed distance collision-avoidance constraints proposed by the authors of TrajOpt. Other robust planners in the literature assume that the robot can be modeled as a point in the task space. This assumption works well for applications where the robot’s body is small compared to its environment (e.g., drones or small car-like robots), but is not suitable for manipulators made of complex geometry. On the other hand, ROMP does not require the sensing uncertainty to be modeled using Gaussian noise (or other specific type of probability distribution). Its only assumption is that the uncertainty of the parameters is bounded and that one can have access to sample from the distribution. Most methods in the literature require the Gaussianity assumption, which may limit their applicability.
At each iteration, ROMP solves the following convex optimization problem:
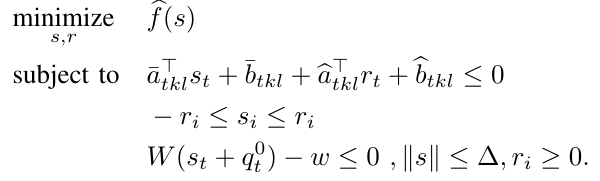
The parameters of this robust formulation need to be estimated at every iteration. This can be achieved by allowing ROMP to sample from the distribution of the noisy objects and keeping the maximum deviation of each parameters from its expected value. ROMP also modifies the actual merit function to account for the additional robust terms being added to the convex subproblems to enable convergence of the SCO algorithm.
Some experiments
We performed experiments to assess the performance of ROMP to a different set of noise models. To this end, we created a nominal scene of the fetch robot example and solved the motion planning problem using RRT-Connect, TrajOpt and ROMP. Then, we evaluated the probability of collision of such trajectories for both Gaussian and Uniform noise for a wide set of the distribution parameters using Monte Carlo experiments for 5000 samples for each distribution. The results can be shown in the figure below:
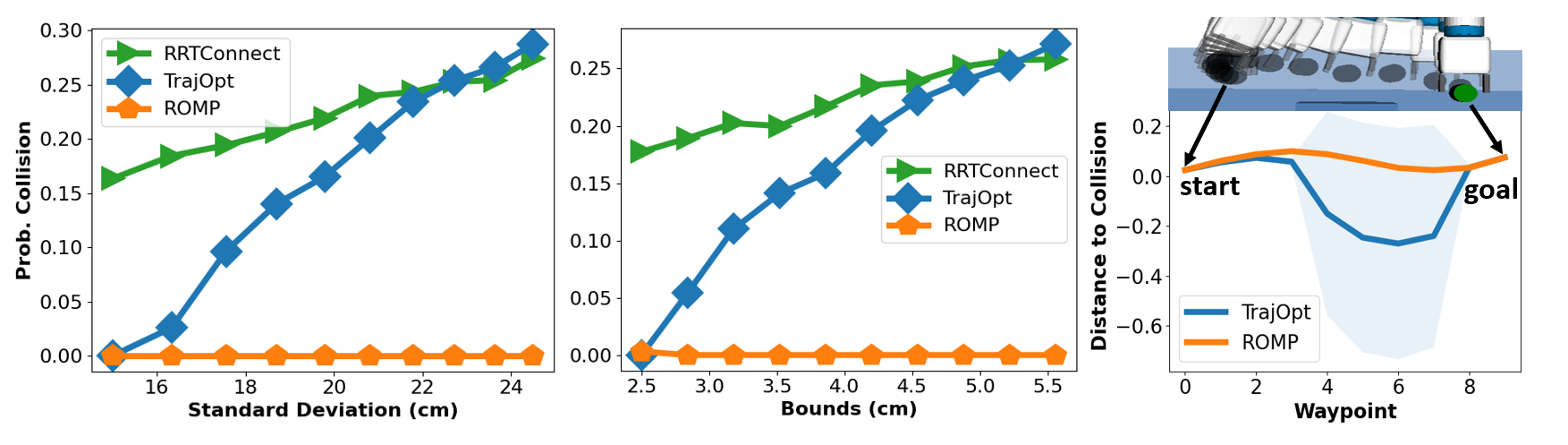
It can be seen that ROMP successfully maintain a low probability of collision for all the distribution parameters (Gaussian on the left, Uniform on the center). Additionally, the figure on the right shows the average distance to collision between the robot and the noisy object for each trajectory waypoint and its standard deviation for both TrajOpt and ROMP.
The figure below show examples of more trajectories computed by the planners for the same task but when the grasp pose is different.
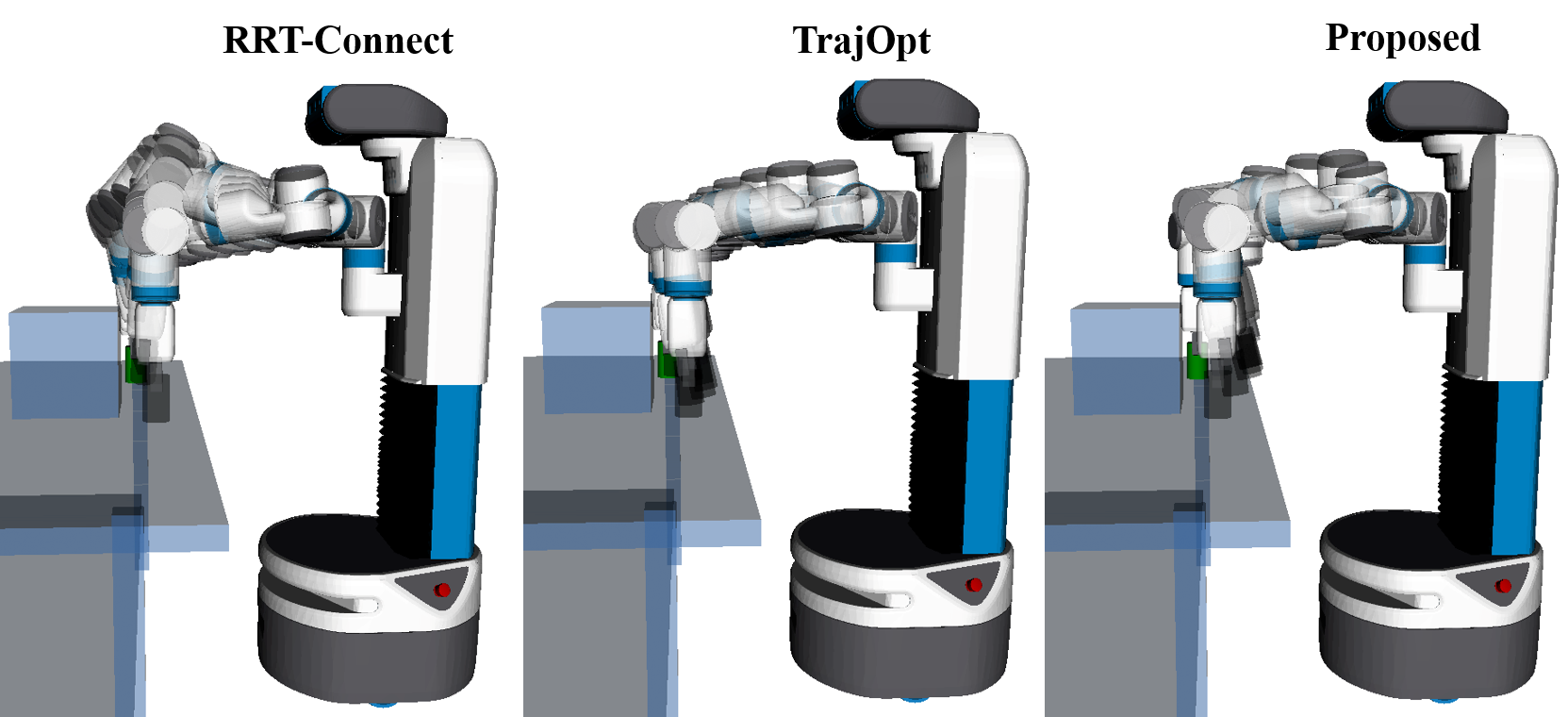
It can be noticed that similar to the previous example, RRT-Connect and TrajOpt find trajectories that go very close to the obstacle. ROMP however, pushes the trajectory closer to the robot’s body to account for the uncertainty in the direction of the noise. The following video shows the trajectory traces.