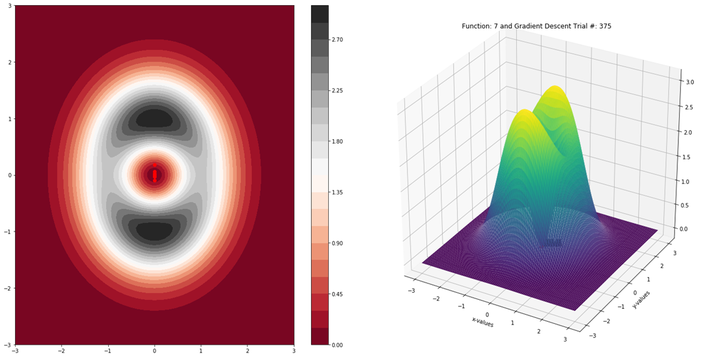
 Gradient Descent gets stuck in saddle points
Gradient Descent gets stuck in saddle points
This project provides a literature review for the most important recent works related to optimizing high-dimensional non-convex functions in the presence of saddle points mostly for machine learning applications.
The inspiration came from reviewing the paper “How to Escape Saddle Points Efficiently?”. A large research effort has been devoted to proposed methods that can converge to second order stationary points efficiently. Of special interest is the set of methods that do not rely on Hessian computation, mainly driven by applications in machine learning where this may not be feasible. Although, many important theoretical results have been proposed, many of them have not be tested in real experiments, especially in the context of training a deep neural network. We have designed experiments with different network architectures and state-of-the-art datasets to observe the behavior of perturbed versions of gradient descent. Initial results show that an improvement in experimental convergence rate can be seen only for small and shallow networks.